The Basics of Lunar Ranging
The basic idea is that we want to test our understanding of gravity to unprecedented precision. The earth-moon system is an ideal laboratory for performing such a measurement. The earth and moon are attracted to each other and to the sun by gravity, so that studying the dynamics of this system is a way to explore the precise behavior of gravity. For instance, we can ask the question: "do the earth and moon fall toward the sun with the same acceleration?" To do this, we need to measure the exact shape of the lunar orbit. We want to measure the earth-moon distance at various points in the lunar cycle (crescent, quarter moon, gibbous, and full phases). Each measurement will be precise to one millimeter—about the thickness of a paperclip. We do this by measuring the round-trip travel time of a light pulse bouncing off lunar reflectors. Multiplying this time by the speed of light gives us the distance. In addition to characterizing the shape of the lunar orbit, we we will be able to follow the slow recession of the lunar orbit by 3.8 cm (1.5 inches) per year due to tidal friction.
One way to state why millimeter-precision measurements help us understand gravity is: any theory of gravity will predict certain specific paths/orbits of the bodies under its influence, given initial conditions. Is general relativity predicting exactly the correct path for the moon? If not, we've got trouble. General relativity (GR) predicts deviations from Newtonian gravity at the several-meter level in the lunar orbit. So millimeter-level measurement precision puts GR to a hard test.
When Einstein came up with his theory of general relativity, he claimed that this was a better description of gravity than Newton's time-tested and very successful model. Many reacted with healthy skepticism—nobody was complaining about deficiencies in Newtonian gravity (at least not many people were). But today, test after test has shown that Newtonian gravity doesn't cut it in ultra-precise tests. It's still good enough to plan interplanetary probe trajectories, but not good enough to describe everything we see. And surprisingly, understanding general relativity is absolutely vital in getting the global positioning system (GPS) to work. This system would utterly fail in an hour's time if we didn't anticipate that time runs more slowly in a gravitational field—a consequence predicted by general relativity.
Today, there is a growing sentiment in the physics and astrophysics communities that general relativity is likely not the last word on gravity. First, GR is not compatible with quantum mechanics. Maybe we live in the kind of universe where we can have two incompatible descriptions of the fundamental rules of how matter behaves and interacts. But past reductions/unifications (e.g., electricity and magnetism; the weak nuclear force and electromagnetism) suggest otherwise. Who would you bet on? Aspects of quantum mechanics have been tested to phenomenal precisions: part-in-a-trillion levels. But GR has been tested only to part-in-100,000 levels so far. It's more likely to be incomplete than is quantum mechanics. And perhaps more convincingly, we now see that the expansion of the universe is accelerating! This is a total surprise, and not consistent with the predictions of general relativity. It is highly likely that the solution to this puzzle will involve a modification to or replacement of general relativity.
Lunar laser ranging has been performed for the past 35 years, now reaching a precision of 2 centimeters. APOLLO (the Apache Point Observatory Lunar Laser-ranging Operation) will improve this performance by at least a factor of ten. While this factor of ten (or better) may not be enough to expose a shortcoming in the theory of general relativity, there is a chance that it will. We can't afford not to look. At the very least, APOLLO will place more stringent constraints on existing and future alternatives to Einstein's theory of gravity. Many new phenomena are discovered in science by looking closely at things we think we understand perfectly, only to find that our knowledge or understanding is incomplete.
How do we measure the distance to the moon to such phenomenal precision? We "ping" the moon with ultra-short pulses of light. To do this, we have a laser that generates intense bursts of light only 100 picoseconds long—that's one tenth of a billionth of a second! Light, which travels 7 earth circumferences every second, only travels about an inch in this time. So these pulses are like little "bullets" of light.
In essence, we measure the time it takes for the pulse of light to travel to the moon and back. This can take anywhere from 2.34 to 2.71 seconds, depending on how far away the moon is at the time (the earth-moon distance ranges from 351,000 km to 406,000 km). We can time the round trip to few-picosecond precision, or a few trillionths of a second.
We measure to the retroreflector arrays left on the moon by the Apollo astronauts, and by an unmanned Soviet rover carrying a French-built reflector. These define very specific points of reference on the lunar surface. This is far better than measuring to the rough-and-tumble surface. We would never have any hope of measuring the lunar distance to millimeter precision without these well-defined reflectors. We aim at one reflector at a time when performing the measurement.
The telescope used for APOLLO has a 3.5 meter diameter mirror, and is located at the Apache Point Observatory in southern New Mexico. We use the telescope as a gigantic (3.5 meter wide) laser pointer and also as a signal receiver. We reference our measurements to the center of the telescope mount, where the azimuth axis and elevation axis intersect each other. As the telescope swings around to point at different parts of the sky, this point stays fixed—almost.... The position of the telescope relative to the center of the earth isn't as stationary as you might imagine. The continental plate drifts, the tides from the moon and sun make the site swell by about a foot twice a day, weather systems can push the local crust down, etc. We have to be aware of all of these influences and take them into account in order to extract the scientifically useful center-to-center distance between the earth and moon.
We will typically measure the distance to each of the four available reflectors in turn over a half-hour period. Then we'll do the same thing a few nights later. By doing this over months and years, we will characterize the shape of the lunar orbit to high enough precision to be able to say something about the workings of gravity.
To concentrate as much laser power as possible onto the reflector array, we must ensure that the beam leaving the telescope is as collimated (parallel, non-diverging) as possible. We use a laser both because we can get ultra-short pulses of light from a laser, and also because the light from a laser is extraordinarily directional—not diverging the way a flashlight, or even searchlight, would. Even so, the turbulent atmosphere distorts the beam, imparting a divergence of about one arcsecond (sometimes more). One arcsecond is 1/3600th of a degree, or the angular size of a quarter about five kilometers (about 3 miles) away. At the distance of the moon, this angle translates to 1.8 kilometers (just over a mile). Though this is large compared to the size of the reflector (most of the light is wasted—never hitting the reflector), it is still a challenge to point and maintain the laser beam on this tiny patch of the moon.
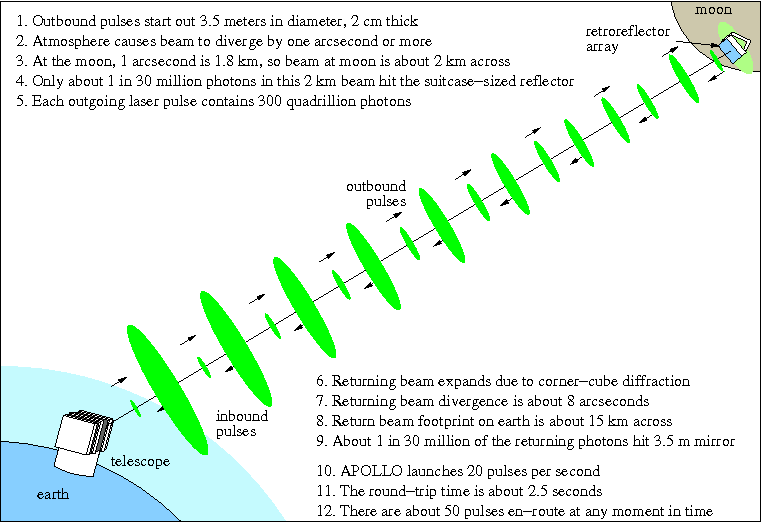
As the above schematic illustrates, the beam we send to the moon diverges (much exaggerated) due to the earth's atmosphere. Only about one part in 30 million of the light we send to the moon is lucky enough to actually strike the targeted reflector. But the reflector is composed of small corner cubes, and for reasons related to the uncertainty principle in quantum mechanics, the light returning from each of these small apertures is forced to have a divergence (called diffraction). In the case of the Apollo reflectors, this divergence is in the neighborhood of 8 arcseconds. This means that the beam returning to the earth has a roughly 15 kilometer (10 mile) footprint when it returns to the earth. We scrape up as much of this as our telescope will allow, but a 3.5 meter aperture will only get about one in 30 million of the returning photons—coincidentally the same odds of hitting the reflector in the first place.
We can't achieve millimeter-range precision from a single photon. Our laser pulse is broader than this (2.5 cm), and we don't know if a particular photon was in the leading or trailing edge of the beam, or right in the middle. Likewise, the slight tilt of the reflector array introduces a similar uncertainty. In all, we have about 30 to 50 millimeters of uncertainty per photon. But if we collect many photons, the average round-trip time for the ensemble will have a higher precision. The statistical rule for this is that the reduction in error one gets by obtaining N independent measurements is the square-root of N. So to get a reduction to one millimeter from 30–50 mm, we need 900–2500 photons, depending mostly on the degree of tilt of the reflector array for that observation. At, say, one photon per pulse, we will get 1200 photons per minute, and should have adequate numbers for a millimeter measurement in a matter of minutes.
It's all fun and games until someone shoots an eye out! Working with a powerful laser demands some attention to safety. We follow strict safety guidelines when working around the laser, wearing protective glasses that only admit one ten-millionth of any laser light hitting them to pass through. But once we have expanded the beam to fill the 3.5 meter telescope aperture, it is far less dangerous—almost eye-safe, in fact (far too weak to cause damage to anything but eyes or sensitive detectors). Nonetheless, we are diligent about not hitting aircraft, which, more than creating an eye-hazard would potentially startle pilots. Some have reacted in horror when we tell them that we are shooting a laser at the moon. "Why would you want to destroy the moon?" Rest assured that 2.3 watts of laser power spread over a 2 kilometer patch on the moon is nothing compared to the sun's 1380 watts per square meter. Not even enough to tickle.
So now we know what we want to do, and how to do it. But that's the easy part. The first hard part is under our belts: we have constructed the apparatus and established initial operation (July 2005). In the fall of 2005, we acquired our first lunar ranges with the system (see full story). We are now working (winter, 2006) to establish a routine operational state (track our progress). In the spring of 2006, the long effort of data collection will begin, and the next hard part begins: making sense of all these measurements!